[toc]
# RISC-V 寄存器
在 RISC-V 中,所有操作数(Operanden)都存储在寄存器中。
RISC-V ISA 拥有 32 或 33 个(可见)寄存器,其中 x0 远为零,而 x1 到 x31 是通用整数寄存器, f1 到 f31 是 浮点寄存器:
| Register | ABI Name | Description | Saver |
|---|---|---|---|
| x0 | zero | Hard-wired zero | — |
| x1 | ra | Return address | Caller |
| x2 | sp | Stack pointer | Callee |
| x3 | gp | Global pointer | — |
| x4 | tp | Thread pointer | — |
| x5–7 | t0–2 | Temporaries | Caller |
| x8 | s0/fp | Saved register/frame pointer | Callee |
| x9 | s1 | Saved register | Callee |
| x10–11 | a0–1 | Function arguments/return values | Caller |
| x12–17 | a2–7 | Function arguments | Caller |
| x18–27 | s2–11 | Saved registers | Callee |
| x28–31 | t3–6 | Temporaries | Caller |
| Register | ABI Name | Description | Saver |
| ------------ | ----------- | ------------------------------------ | --------- |
| f0–7 | ft0–7 | FP temporaries | Caller |
| f8–9 | fs0–1 | FP saved registers | Callee |
| f10–11 | fa0–1 | FP arguments/return values | Caller |
| f12–17 | fa2–7 | FP arguments | Caller |
| f18–27 | fs2–11 | FP saved registers | Callee |
| f28–31 | ft8–11 | FP temporaries | Caller |
这里第一列的是每个寄存器的编号,而第二列则是附带语义的名字。一般在汇编代码中使用 ABI name,便于理解和维护。
关于 Saver 部分可以看下面这个表,会更直观一点:
| Name | Meaning | Saver | Preserved across calls? |
|---|---|---|---|
| ra | Return address | Caller | No |
| sp | Stack pointer | Callee | Yes |
| t0 - t6 | Temporary registers | Caller | No |
| s0 - s11 | Callee-saved registers | Callee | Yes |
| a0 - a7 | Argument registers | Caller | No |
Caller 指的是调用函数的一方(比如说 main ()),而 Callee 指的则是被调用的函数。
如果一个 register 的 Saver 是 Caller,则调用函数的一方(Caller)需要在调用函数前将这些寄存器里的值都存储好,以便被调用函数可以随意使用;
如果一个 register 的 Saver 是 Callee,则被调用函数需要确保这些寄存器的值在该函数结束后与之前一模一样。
通俗一点来讲,前者是将自己的笔记本备份好之后借出去,借用方(Callee)可以随意使用;后者则是将笔记本借出去,但借用方必须确保拿到的时候是什么样子的还回去的时候也得是什么样子的。
# RISC-V 汇编语言
每一个 ISA(Instruction Set Architecture)的指令都可以分为以下 3 大类:
-
算术和逻辑运算(Arithmetische und logische Operationen) -
数据传输(Datentransfer) -
程序控制 (Steuerung des Programmablaufs):跳转和子程序调用( Sprünge und Unterprogrammaufrufe)
RISC-V 汇编指令一览:
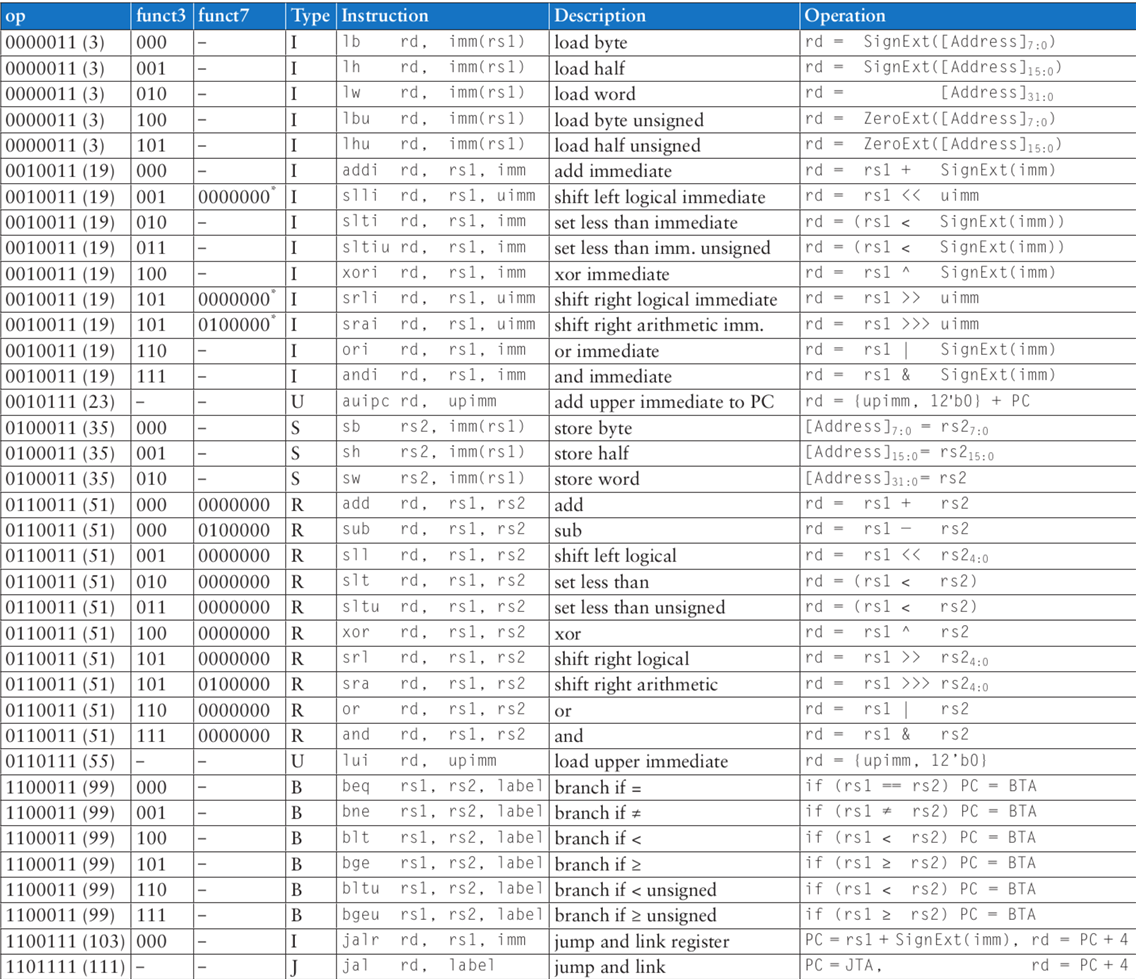
# 算术 Arithmetik
加法:
a = b + c
add a,b,c
减法:
a = b - c
sub a,b,c
组合:
a = b + c - d
add t,b,c # t=b+c
sub a,t,d # a=t-d
浮点数的情况:
"f" 用于 Single Precision (32bit) Gleitkomma;
"d" 用于 Double Precision (64bit) Gleitkomma。
fadd a,b,c
fsub a,b,c
dadd a,b,c
dsub a,b,c
乘法的话基本上就是以下几种:

只不过 RISC-V 的基本整数指令集中(RV32I 和 RV64I)不包含 mul 指令,乘法运算通常需要 M 扩展(RV32M/RV64M)。如果只允许使用 RV32I/RV64I 指令,则必须通过移位和加法手动实现乘法。
在硬件实现上,移位操作比乘法更快,因为移位仅涉及逻辑电路,而乘法通常需要额外的计算资源。
例子:
假设
$ s2 = 0x80000000 = -2^{31}$
$ s1 * s2 = -2^{61} = 0xE0000000 00000000$
那么
mul s3, s1, s2
mulh s4, s1, s2
# {s4,s3} = s1 * s2
便会得到
$ s4 = 0xE0000000; s3 = 0x00000000$
除法以及余数:


# 逻辑运算 Logische Operation
和:
a = b AND c
and a,b,c
或:
or a,b,c
异或:
xor a,b,c
移位(Shifts):
移位操作分为 2 种:
1. 逻辑移位 logischer Shift ,用 >>, << 表示
用 0 填充空出的高位,无论原数是正数还是负数 (Null Bits nachgeführt),适用于 无符号数(unsigned numbers) 计算。
例子 1:
假设
t0 = 1111 1111 1111 1111 1111 1111 1110 0111 = -25(补码表示)
那么经过
srl t0, t0, 4
会得到
t0 = 0000 1111 1111 1111 1111 1111 1111 1110 = 268435454(正数)
例子 2:
假设
t0 = 0000 0000 0000 0000 0000 0000 0001 1001 # 25(十进制)
那么经过
sll t0, t0, 4
会得到
t0 = 0000 0000 0000 0000 0000 0001 1001 0000 = 400(正数)
()
2. 算术移位 arithmetischen Shift ,用 >>>, <<< 表示
会保持符号位(MSB)不变 (erhält Vorzeichen, 0 oder 1 nachgeführt)
- 如果是正数(MSB = 0),则用 0 填充高位。
- 如果是负数(MSB = 1),则用 1 填充高位。
适用于 有符号数(signed numbers) 计算,保持符号正确。
例子 1:
假设
t0 = 1111 1111 1111 1111 1111 1111 1110 0111 = -25(补码表示)
那么经过
sra t0, t0, 4
会得到
t0 = 1111 1111 1111 1111 1111 1111 1111 1110 = -2 (负数)
左移本质上就是乘法。无论有符号数还是无符号数,左移的行为都是相同的,所以 RISC-V 没有 sla 令。
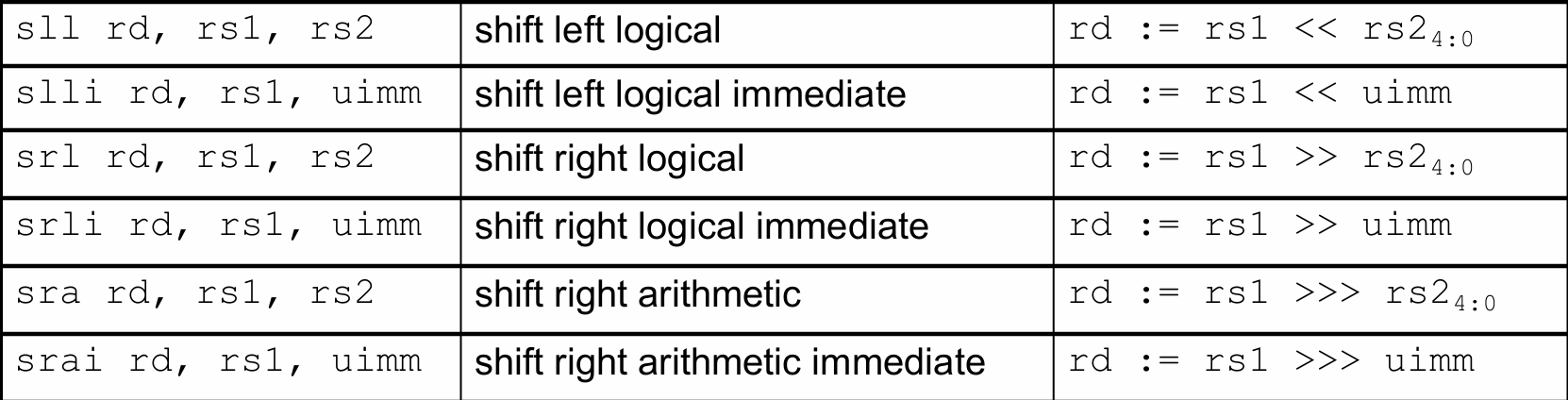
这里的 uimm 会被限制在 5-bit 的无符号整数。
# 数据传输(Datentransfer)
读取(Lesen vom Speicher):
ld (load word)
Format:
ld destination, offset(base)
例子:
ld a1, 8(s0)
Basisadresse (s0) zum Offset (8) addieren,
Adresse = ([Wert in s0] + 8)
写入(Schreiben in den Speicher):
sd (store word)
Format:
sd source, offset(base)
例子:
ld a1, 8(s0)
Basisadresse (s0) zum Offset (8) addieren,
Adresse = ([Wert in s0] + 8)
# 跳转 Sprung
无条件跳转:
j imm
jr reg, imm
第一个会跳转到 PC = PC + imm
第一个会跳转到 PC = reg + imm
有条件跳转:
格式:
bxx r1,r2,imm
bxx 的可选选项:
branch if equal (beq):
branch if not equal (bne):
branch if less than (blt):
branch if greater than or equal (bge):
例子 1(if):
if (i == j){ | |
f = g + h;} | |
f = f – i; |
跟上面这段 c 代码等价的 RISC-V Assembler(汇编):
# s0 = f, s1 = g, s2 = h
# s3 = i, s4 = j
bne s3, s4, L1
add s0, s1, s2
L1:
sub s0, s0, s3
例子 2(if, else):
if (i == j){ | |
f = g + h;} | |
else{ | |
f = f - i;} |
跟上面这段 c 代码等价的 RISC-V Assembler(汇编):
# s0 = f, s1 = g, s2 = h
# s3 = i, s4 = j
bne s3, s4, L1
add s0, s1, s2
j done
L1:
sub s0, s0, s3
done:
例子 2(while 循环):
// Berechne x, so dass | |
// 2^x = 128 | |
int pow = 1; | |
int x = 0; | |
while (pow != 128) { | |
pow = pow * 2; | |
x = x + 1; | |
} |
跟上面这段 c 代码等价的 RISC-V Assembler(汇编):
# s0 = pow, s1 = x
addi s0, zero, 1
add s1, zero, zero
addi t0, zero, 128
while:
beq s0, t0, done
slli s0, s0, 1
addi s1, s1, 1
j while
done:
# 子程序调用 Unterprogramme
Begriffe:
Caller(调用者):调用函数的代码(如 main ())。
Callee(被调用者):被调用的函数(如 simple ())。
jal reg, offset #调用
jr ra #返回
例子:
int main() { | |
simple(); | |
a = b + c; | |
} | |
void simple() { | |
return; | |
} |
跟上面这段 c 代码等价的 RISC-V Assembler(汇编):
0x00000300 main: jal simple # call
0x00000304 add s0, s1, s2
... ...
0x0000051c simple: jr ra # return
其他的伪命令:
mv ra, rb
跟
add ra,rb,x0
addi ra,rb,x0
等价。
# 递归(Rekursion)
# 普通递归
例子 1:阶乘
int factorial(int n) { | |
if (n == 0) return 1; | |
return n * factorial(n - 1); // (递归调用后还有乘法,所以是非尾递归) | |
} |
对应的 RISC-V(n=4 的情况示例):
_start:
0x200 addi a0, zero, 4 # a0 = 4,计算 4 的阶乘(作为输入参数)
0x204 jal ra, magic # 跳转调用 magic 函数(递归实现阶乘),返回地址存入 ra
0x208 ebreak # 程序断点(模拟器中用于停止执行)
magic:
0x20c beq a0, zero, break # 如果 a0 == 0,跳转到 break(0! = 1)
0x210 addi sp, sp, -8 # 分配栈空间:只保存 ra 和 a0,所以是2*4=8Bits
0x214 sw ra, 0(sp) # 保存返回地址 ra 到栈顶
0x218 sw a0, 4(sp) # 保存当前参数 a0(n)
0x21c addi a0, a0, -1 # a0 = a0 - 1,准备递归调用 magic(n-1)
0x220 jal ra, magic # 递归调用 magic(n-1),返回值仍存在 a0 中
0x224 lw t0, 4(sp) # 从栈中恢复原来的 a0(也就是 n)
0x228 mul a0, a0, t0 # a0 = a0 * n(也就是 n! = n * (n-1)!)
0x22c lw ra, 0(sp) # 恢复之前保存的返回地址
0x230 addi sp, sp, 8 # 回收栈空间
0x234 jalr zero, 0(ra) # 返回调用者(函数返回)
break:
0x238 addi a0, zero, 1 # a0 = 1,返回 1(0! = 1)
0x23c jalr zero, 0(ra) # 返回调用者
由于每次计算 factorial(n) 的值时需要先等 factorial(n-1) 计算结果先出来,所以等待期间需要将所有的 n 都给存在 stack 里,也就是说:
factorial(4) | |
→ 需要等factorial(3) 的结果 | |
→ 需要等 factorial(2) 的结果 | |
→ 需要等 factorial(1) 的结果 | |
→ 需要等 factorial(0) 的结果 | |
→ 返回 1 | |
然后开始回溯计算: | |
factorial(1): 1 * 1 = 1 | |
factorial(2): 2 * 1 = 2 | |
factorial(3): 3 * 2 = 6 | |
factorial(4): 4 * 6 = 24 |
而栈结构如下:
+--------------------+ | |
| 0x4 | | |
| 0x208 | | |
+--------------------+ | |
| 0x3 | | |
| 0x224 | | |
+--------------------+ | |
| 0x2 | | |
| 0x224 | | |
+--------------------+ | |
| 0x1 | | |
| 0x224 | | |
+--------------------+ |
返回的时候则是这样:
当 a0=0 的时候触发 0x20c 的 beq,跳转到 break,break 执行完了会跳转到当前的 ra(也就是 stack 最底下一行的 0x224),然后进行这部分操作:
0x224 lw t0, 4(sp) # 从栈中恢复原来的 a0(也就是 n)
0x228 mul a0, a0, t0 # a0 = a0 * n(也就是 n! = n * (n-1)!)
0x22c lw ra, 0(sp) # 恢复之前保存的返回地址
0x230 addi sp, sp, 8 # 回收栈空间
0x234 jalr zero, 0(ra) # 返回调用者(函数返回)
计算 a0 = 1*1 然后继续跳转到 stack 倒数第三行的 0x224,重复下去知道跳转到 0x208,触发断点。
例子 2:最大公约数
unsigned ggT(unsigned a, unsigned b) { | |
if (a == b) | |
return a; | |
else if (a < b) | |
return ggT(a, b - a); | |
else | |
return ggT(a - b, b); | |
} |
对应的 RISC-V:
ggT:
beq a0, a1, finished # 如果 a0 == a1,则跳转到 finished(返回结果)
bltu a0, a1, lt # 如果 a0 < a1,则跳转到 lt 标签(交换顺序)
sub a0, a0, a1 # 否则 a0 > a1,执行 a0 = a0 - a1
j cont # 跳转到 cont,准备递归调用
lt:
sub a1, a1, a0 # 执行 b = b - a (即 a1 = a1 - a0)
cont:
addi sp, sp, -16 # 为返回地址创建栈空间(递归调用前保存返回地址)
sw ra, 0(sp) # 保存返回地址
jal ra, ggT # 递归调用 ggT(jump and link)
lw ra, 0(sp) # 恢复返回地址
addi sp, sp, 16 # 回收栈空间
jalr zero, 0(ra) # 返回(跳转回上层调用)
finished:
jalr zero, 0(ra) # 返回当前的 a0 作为结果
总结一下:
每个 Recursive 的函数递归部分会分成 2 部分:
- 从当前 n 的情况跳转到 n-1,保存当前 n 的值以及返回地址(即当前跳转命令的下一行的地址)
- 读取返回地址并用当前已经计算出来的 n-1 的情况的值与 n 进行函数运算。
相当于递减完了之后还得递增回来。
注意,2 个例子里分配的 stack 的大小是不一样的,这个主要是看 ABI 的具体要求,这里主要目的是示范而已。但不管大小如何,一定要保证分配的 Stack 大小和回收的大小是一致的。
# 尾递归(Tail Rekursiob)
观察上面例子里 stack 存储的内容不难发现,如果递归的次数较高,则会很容易导致 Stack Overflow。
为了解决这个问题,我们可以使用另一种递归方式: 尾递归(Tail Rekursiob)
还是拿阶乘举例,我们将代码优化成这样:
int factorial(int n, int acc = 1) { | |
if (n == 0) return acc; | |
return factorial(n - 1, n * acc); // 尾调用 | |
} |
对应的 RISC-V:
factorial:
beqz a0, end_factorial
mul a1, a0, a1 # acc = acc * n
addi a0, a0, -1 # n = n-1
tail factorial # 尾调用(跳转,无需保存返回地址)
end_factorial:
mv a0, a1 # 返回结果
ret
这里的调用过程则会变成:
factorial(3, 1) | |
→ 直接 tail call 到 factorial(2, 3) | |
→ 再 tail call 到 factorial(1, 6) | |
→ 再 tail call 到 factorial(0, 6) | |
→ 结束:返回 acc = 6 |
栈结构如下:
+--------------------+ | |
| 当前调用(复用栈帧)| | |
| n=3, acc=1 | | |
→ tail call → 替换为: | |
| n=2, acc=3 | | |
→ tail call → 替换为: | |
| n=1, acc=6 | | |
→ tail call → 替换为: | |
| n=0, acc=6 | | |
→ return 6 |
不再需要存储所有中间的 n 的值。相当于是直接跳转而不是等待。
# 带有立即数(immediate)的命令
立即数(Immediate/Konstante) :由指令本身携带,不需要从寄存器或内容中加载
aadi
a = b + imm(一个立即数)
addi a,b,<imm>
注意,RISC-V 里是没有 subi 这种操作的,因为它可以被 addi 代替:
subi a,b,x 是等价于 addi a,b,-x 的(这里的 x 是一个立即数 / 常数)。
但 sub 不可以被 add 替代,是因为 sub a,b,-c 这个操作不合规(c 是一个 register,不存在 - c 这种操作)。
这里可以使用的立即数的大小会被限制在 (具体原因会在之后机器码的部分阐述)
生成 32-Bit 的常数:
需要用到 load upper immediate (lui) 和 addi
lui 的作用是将一个常数加载到目标寄存器的高 20 位(也就是 5Bytes),并将低 12 位(4Bytes)填充为 0。
而 addi 负责将低 12 位(4Bytes)的数值加到目标寄存器中。
例子:
C:
int a = 0xFEDC8765; |
对应的汇编:
# s0 = a
lui s0, 0xFEDC8 # s0 = 0xFEDC8000
addi s0, s0, 0x765
# RISC-V 机器码 Machine Code/Instrunction
将汇编语言翻译成机器码主要依靠下面这 2 张表:

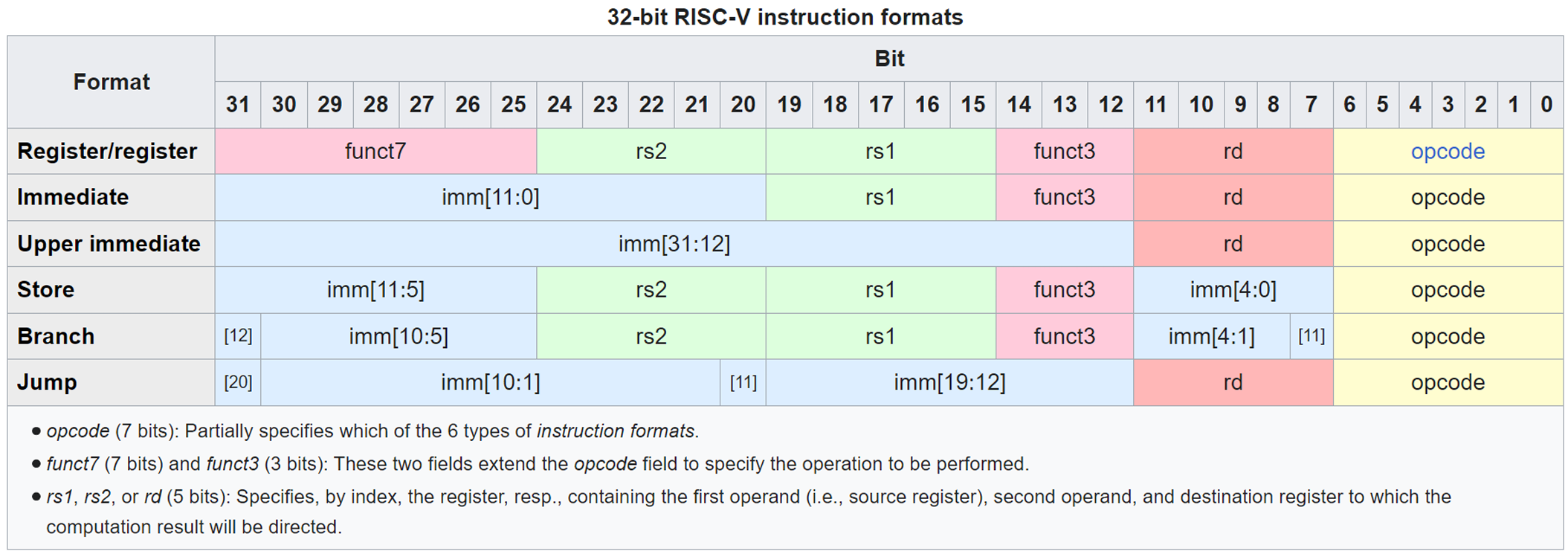
首先,所有的操作会被分成 6 个大类:
- Register/register (R)
- Immediate (I)
- Upper immediate (U)
- Store (S)
- Branch (B) 条件跳转
- Jump (J)
然后会通过 funct3 以及 funct7 确定具体操作。(funct7 更多的是为了扩展的操作 / 功能。)
rs1, rs2, rd 存储的是寄存器的地址,而 imm 存储的则是立即数(immediate)的数值。其中 rd 是目标寄存器。
例子:
addi a1, a2,1
假设 a1(rd),a2(rs1)的地址为 00010,01010,
因为 addi 指令的 opcode 和 funct3 为:0010011, 000 ,这行命令会翻译成以下的机器码:
imm[11:0] | rs1 | funct3 | rd | opcode
------------|-------|--------|-------|--------
000000000001| 01010 | 000 | 00010 | 0010011
S,T,J 那部分内容将 imm 的值拆成好几部分是为了其他内容的位置可以对齐,比如说 rs2 的位置都是第 20-24bit。
Branch 和 Jump 都是跳转操作,所以会将 imm(跳转地址)的第一位(符号位)imm [12] 或者 imm [20] 放在开头,以确定是向后跳转还是向前。然后因为 RISC-V 的命令都是 32 位的,也就是 4Byte,所以所有地址都是 4 的倍数,也就不需要 imm [0] 的信息了,因为 imm [0] 始终等于 0。
# 例题
# 1. Register s5 nullen 将寄存器 s5 的值设为 0:
mov s5, 0
#或者是
li s5, 0
# 2. Wert in Register a1 nach s3 kopieren 将 s3 的值复制到 s1 里:
mv s3, a1
# 3. Dasunterste Bit von a0 nach t1 schreiben, restliche Bits sollen 0 sein 将 a0 的最低位写入 t1,其他位清零:
andi t1, a0, 1
1 在二进制中只有最后一位是 1,其他位置都是 0,所以 a0 的其他位置与 0 进行 and 操作都会得到 0,而最后一位与 1 进行 and 操作会保留原本内容。
# 4. Register s1 mit Einsen füllen 将寄存器 s1 的值为全都是 1:
li s1, -1
因为 - 1 的二进制表示全 1
# 5. Unterstes Byte von t0 nach a0 schreiben, Rest unverändert 将 t0 的最低字节写入 a0,保持其余部分不变:
andi a0, a0, -256 # 清除 a0 的最低字节 (0xFFFFFF00)
or a0, a0, t0 # 直接合并 t0 低字节
-256 的二进制表示为
1111 1111 1111 1111 1111 1111 0000 0000
最后一个 Byte 的内容都是 0,所以将它与 a0 进行 and 操作可以清除 a0 的最后一个 Byte 的内容,前面的保留。
然后将 a0 和 t0 直接进行 or 操作,会保留 a0 的前面部分,以及 t0 的最后一个 Byte 的内容。